三（第5/5页）

当天，吃过晚饭，我们举行了作业解答报告会。博士坐在餐桌旁，我和平方根手里拿着写生簿和万能笔在他面前站好，开始前首先向他鞠了一躬。

“呃——博士出的作业是这样的，把从1到10的数字相加，结果等于多少……”

平方根的态度前所未有地认真。他清了下嗓子，接着按照我们昨晚事先商量好的，在我举着的写生簿上，把从1到9的数字横向排成一排，再隔开一段距离单独写下10。然后他接着说：“答案已经知晓，是55，是我通过加法运算求得的，但博士对此并不满意。”

博士双手抱胸，不愿听漏无论哪个词似的认真地侧耳倾听。

“首先让我们光看从1到9这9个数字，先暂时把10给忘掉。从1到9的正中间是5，就是说，5是……呃……”

“平均数。”我凑到他耳边轻轻提醒道。

“啊，对对，是平均数。求平均数的方法学校里还没学到，是妈妈教我的。把从1到9相加，再除以9等于5……因此，5×9＝45。这就是从1到9的数字之和。现在我们可以把刚才忘掉的10重新想起来了。”

5×9＋10＝55

平方根把万能笔重新握握好，添上了算式。

博士半晌未动。他双手抱胸，一言不发，凝视着算式。

归根结底，自己的所谓灵感只不过是一个幼稚的笑话罢了，我想。虽然早有自知之明，无论再怎么拼命集中精力研究，这一堆乏善可陈的脑细胞里所能榨取的东西，到底有限。而且还企图借此取悦一位数学家，这本来就是狂妄自大……

这时，博士猛地站起身，啪啪鼓掌。他的掌声温暖而强有力，令人想到恐怕连证明了费马大定理的人，也不可能受到这般热烈的称赞。掌声响彻屋内，久久不息。

“精彩极了！多么美丽的一道式子！精彩极了，平方根！”博士紧紧地抱住了平方根。在博士怀中，他的身体被挤得几乎只剩下一半厚度了。“棒极了！没想到从你手中能产生这样的式子……”

“嗯，我知道了，博士，可以了，我要窒息了。”但他的嘴被西装堵住了，声音含混不清，要传到博士耳朵里非常困难。

博士怎么都表扬不够。他禁不住竭尽全力让此刻眼前这名头顶平平、瘦弱的小小少年明白，他自己编写的式子是何等的美妙。

我站在独享称赞的平方根身边，心中喃喃自语道：其实，真正编出那道式子的不是平方根，是我。此时我早忘了刚才还丧失自信、满心别扭的自己，代之以充满了自豪感。我再一次把目光投向写生簿，望着平方根写的那一行。

5×9＋10＝55

虽然我没有正正经经地学过数学，但也知道，这种时候假如用上符号，会显得更高深。

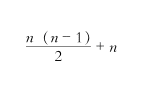
我都佩服我自己了。

与自己误入歧途时的混沌相比，如今抵达的解决之地的这一份清朗又是什么呢？简直仿佛从荒野的洞窟里挖掘出了一小块水晶，不是吗？而且没有一个人能够损伤水晶，也无法否定它。我把博士没表扬我的话都用来孤芳自赏、沾沾自喜。

平方根终于获得了解放。为了回应博士的掌声，我和平方根像在数论学会做完报告的数学家那样，饱含着自豪和感激之情朝他鞠躬致意。

那天，阪神虎以2比3输给了中日龙。和田好不容易靠一支三垒打抢先夺得2分，但对方紧接着连续打出全垒打追平比分，结果形势逆转，阪神虎到底输了。

(1)即埃米尔·阿廷（Emil Artin，1898—1962），奥地利代数学家，在类域论、超复数及拓扑学等领域均作出重大贡献。

(2)丢番图（Diophantos，约246—330）：古希腊代数学家，发表第一部代数学著作《算术》，被后人称为“代数学之父”。